In my Math Modeling course last Fall 2015, we studied an optimization algorithm known as gradient descent. The main application is to find minimizers of functions or functionals. More on the latter later.
Let $F(\mathbf{x})$ be a function defined and differentiable on some domain $\Omega \subseteq \mathbb{R}^n$. Then, gradient descent is the following iterative scheme:
$$
\mathbf{x}^{n+1} = \mathbf{x}^n -\delta \nabla F(\mathbf{x}^n) \ \ \ (1)
$$
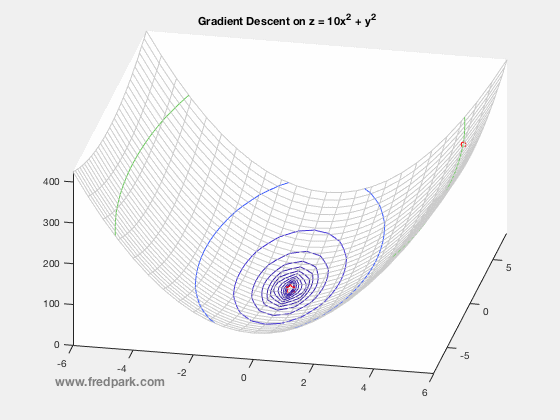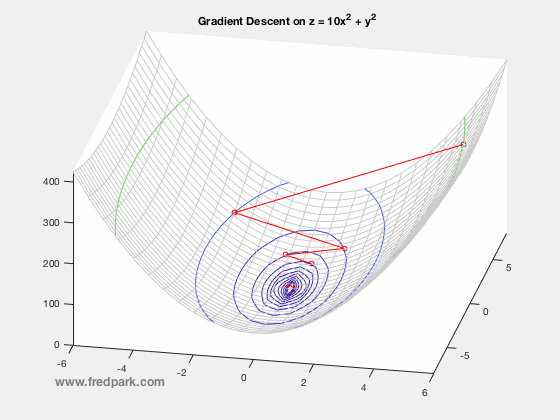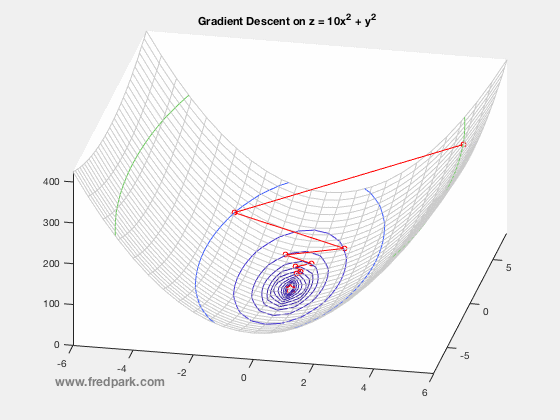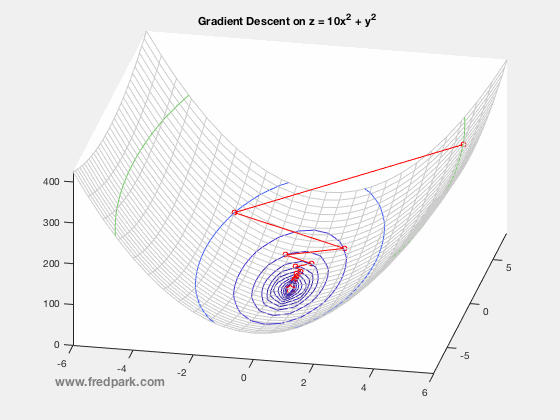
where $\, \delta$ is a time-step parameter and $\, \nabla F(\mathbf{x})$ denotes the gradient of $\, F$. From multi-variable calculus, we know that for a function of 2 variables $z=F(x,y)$ with graph in $\mathbb{R}^3$, the gradient vector points in the direction of steepest ascent of the function $\, F$. Thus, $-\nabla F$ points in the steepest descent direction. This is the key premise of gradient descent. The method is local in nature and for a sufficiently well behaved function ($\nabla F$ Lipschitz continuous), will always move towards a minima from the point obtained from the previous iteration. Thus, it will always converge in that case. Notable caveats include slow convergence near minima, linear convergence rate at best, and non-optimal convergence if the Hessian Matrix is ill-conditioned. An example of slow convergence due to a zig-zagging phenomenon is observed below.
Let $F(\mathbf{x})$ be a function defined and differentiable on some domain $\Omega \subseteq \mathbb{R}^n$. Then, gradient descent is the following iterative scheme:
$$
\mathbf{x}^{n+1} = \mathbf{x}^n -\delta \nabla F(\mathbf{x}^n) \ \ \ (1)
$$
where $\, \delta$ is a time-step parameter and $\, \nabla F(\mathbf{x})$ denotes the gradient of $\, F$. From multi-variable calculus, we know that for a function of 2 variables $z=F(x,y)$ with graph in $\mathbb{R}^3$, the gradient vector points in the direction of steepest ascent of the function $\, F$. Thus, $-\nabla F$ points in the steepest descent direction. This is the key premise of gradient descent. The method is local in nature and for a sufficiently well behaved function ($\nabla F$ Lipschitz continuous), will always move towards a minima from the point obtained from the previous iteration. Thus, it will always converge in that case. Notable caveats include slow convergence near minima, linear convergence rate at best, and non-optimal convergence if the Hessian Matrix is ill-conditioned. An example of slow convergence due to a zig-zagging phenomenon is observed below.
 RSS Feed
RSS Feed