In Calculus I (Math 141A) we are learning Newton's Method. It all starts with a simple linear approximation to a function and seeing where the approximation crosses the x-axis. That crossing point yields a new starting point for another linear approximation and an iterative scheme is created.
$$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}.$$
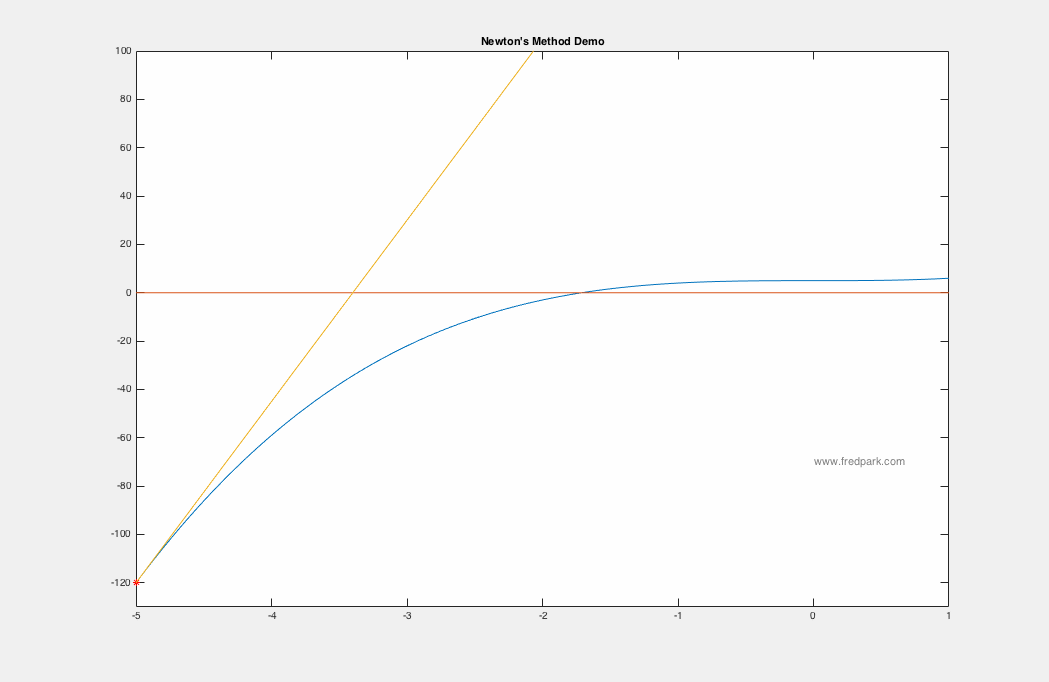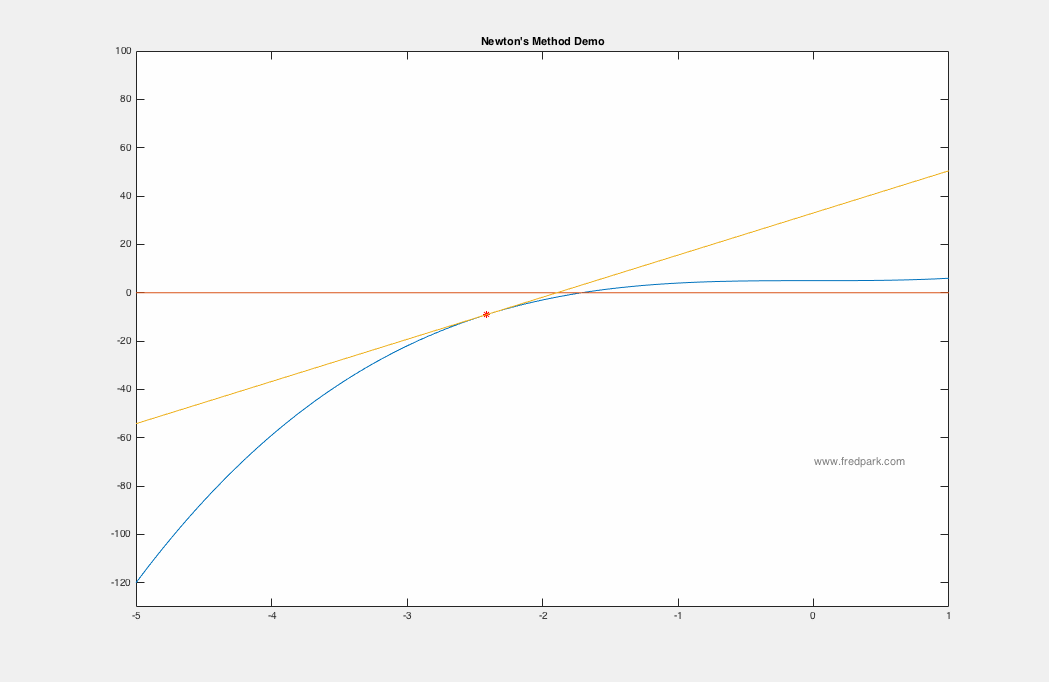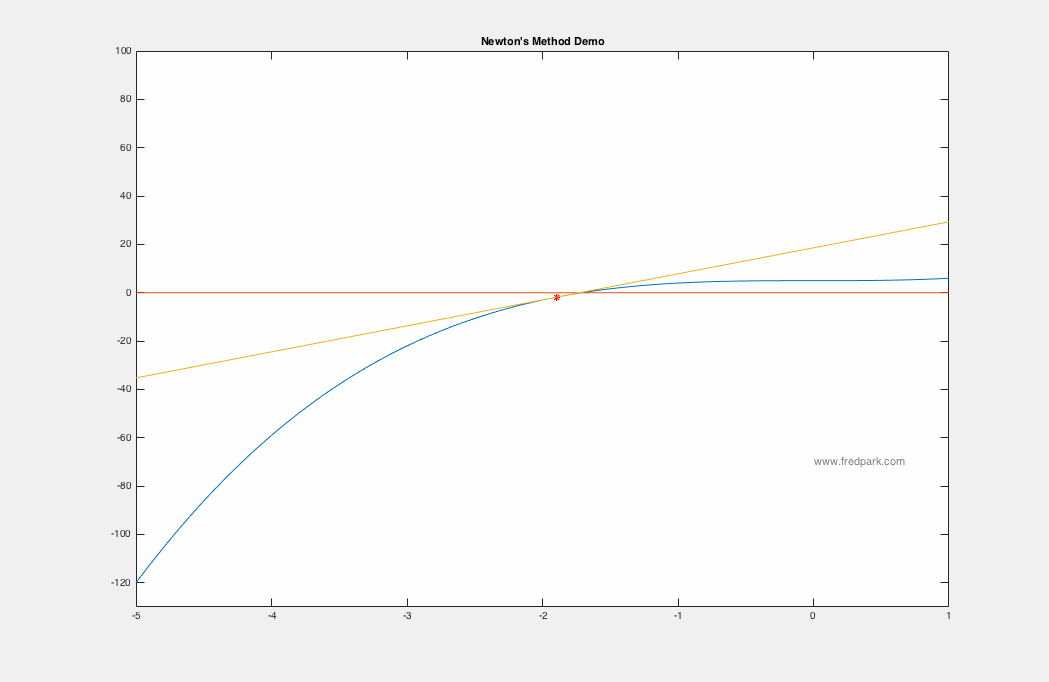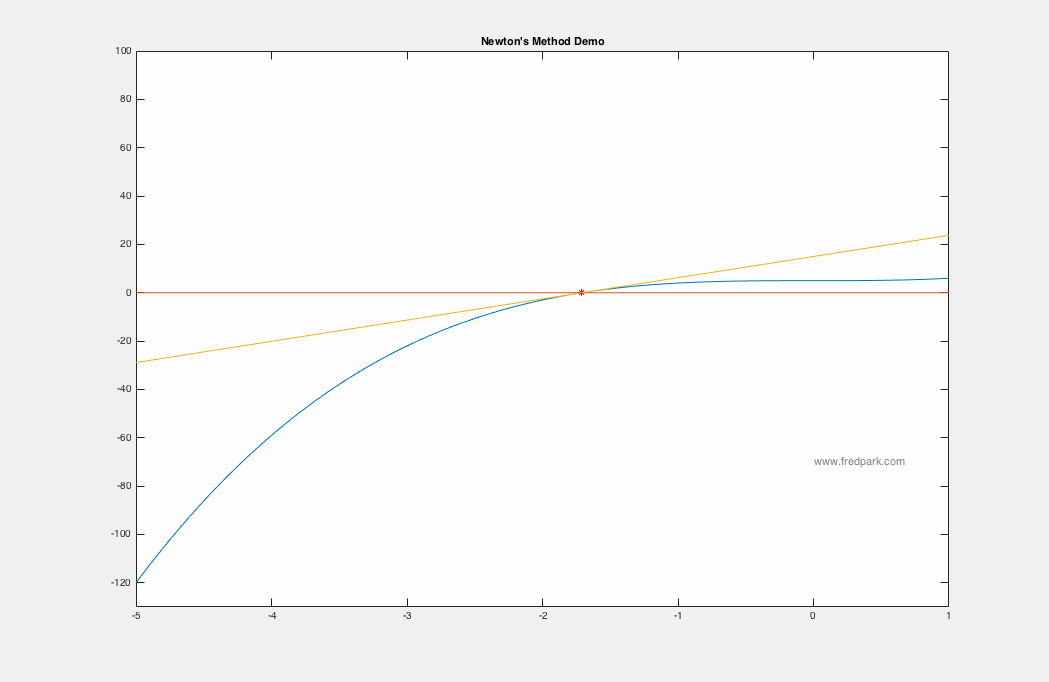
Newton's method applied to the function $f(x) = x^3 + 5$ is seen below using the starting point $x_0 = -5$. Within 7 iterations, $|f(x_7)|<10^{-15}$.
$$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}.$$
Newton's method applied to the function $f(x) = x^3 + 5$ is seen below using the starting point $x_0 = -5$. Within 7 iterations, $|f(x_7)|<10^{-15}$.
 RSS Feed
RSS Feed